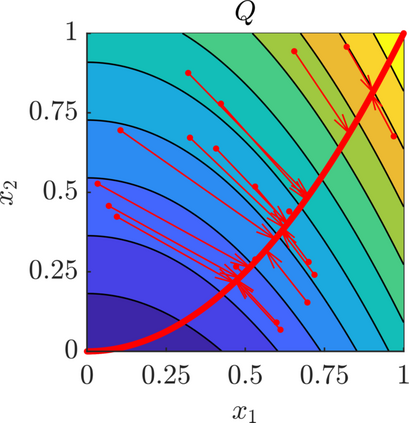
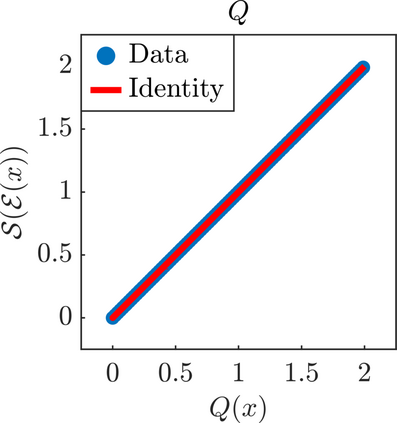
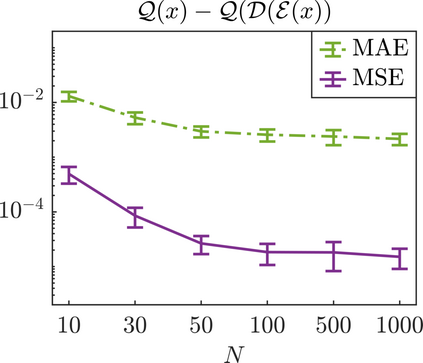
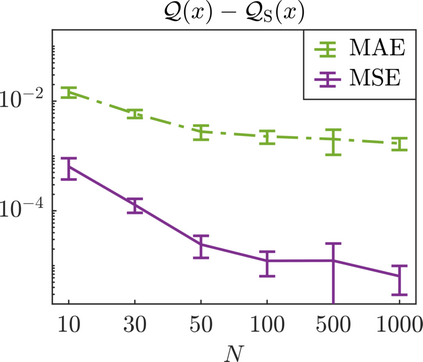
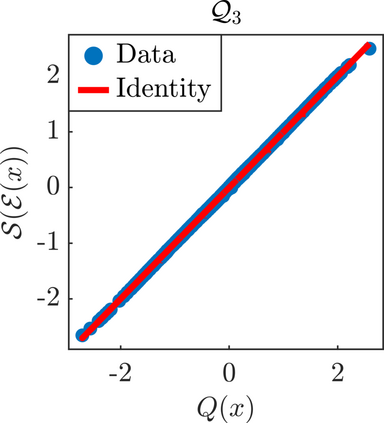
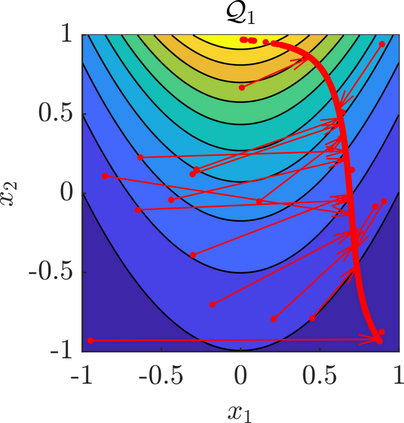
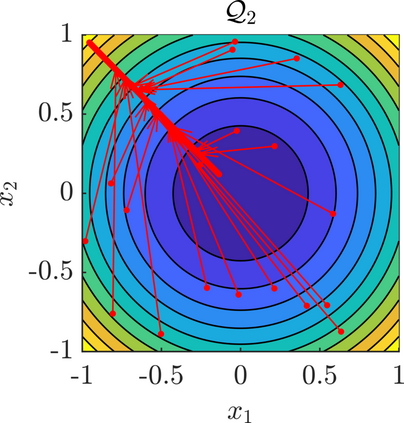
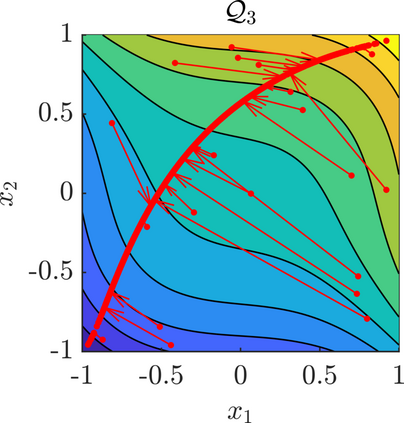
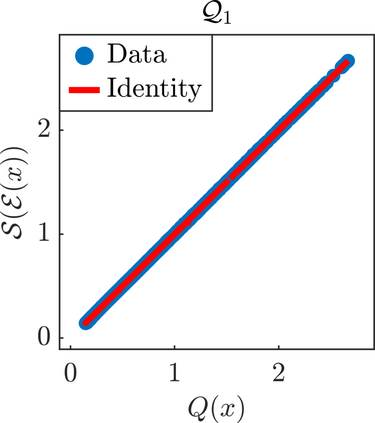
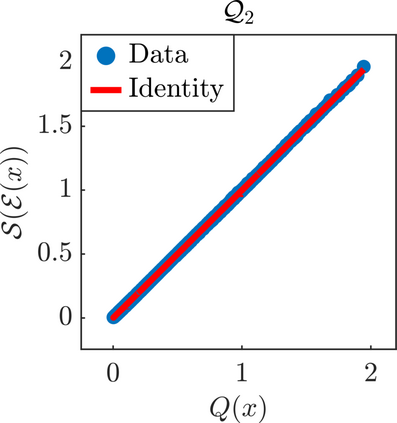
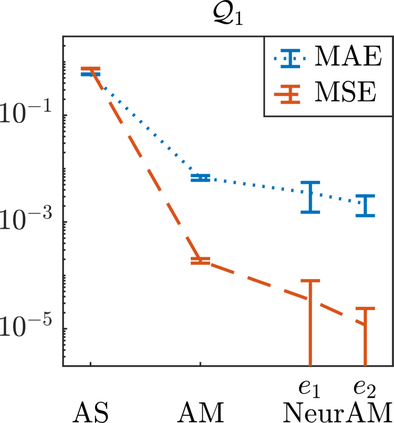
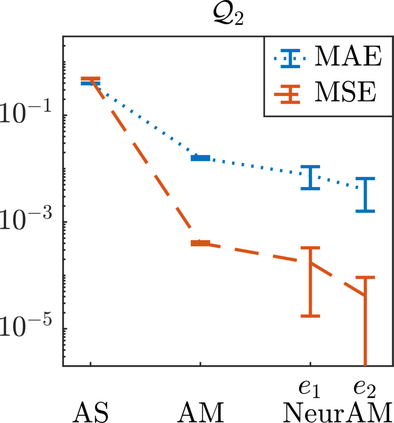
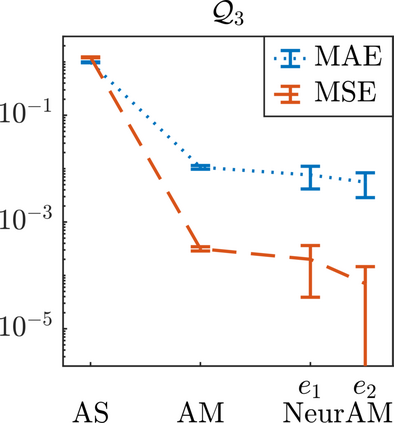
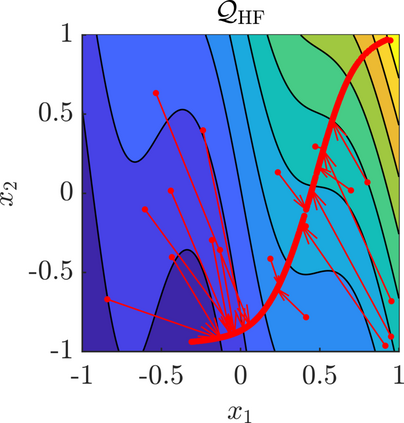
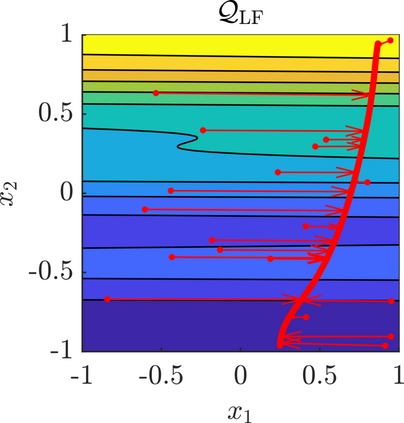
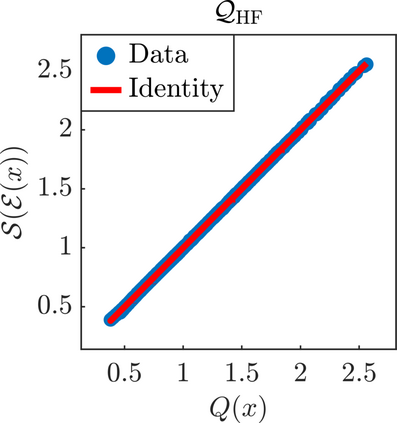
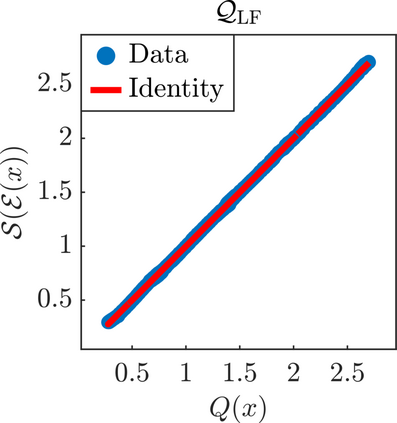
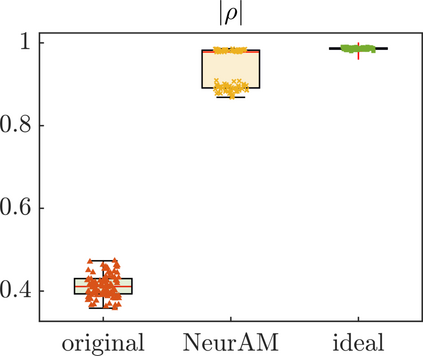
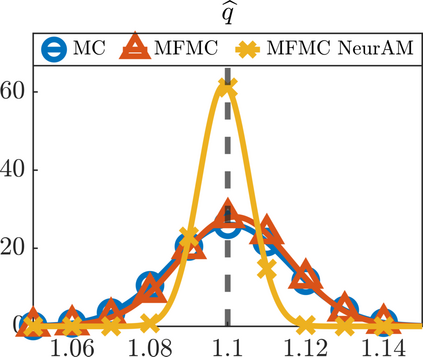
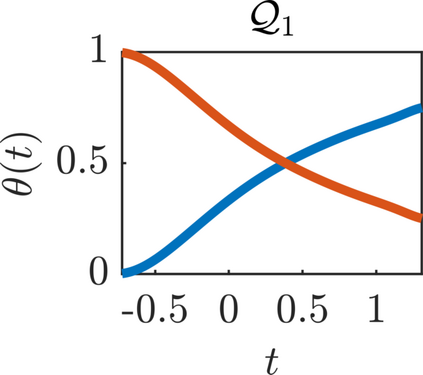
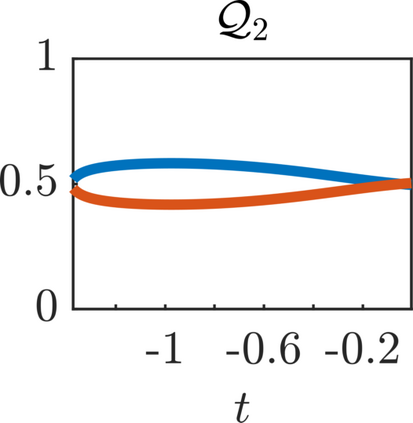
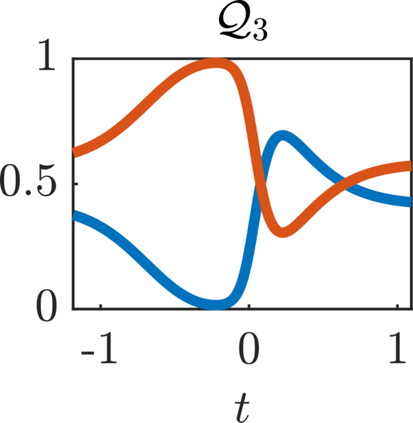
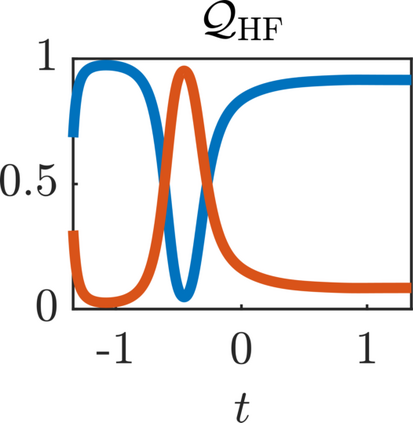
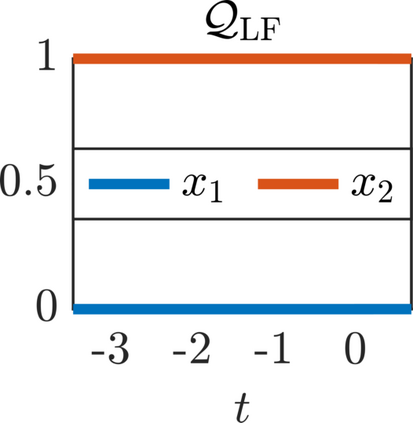
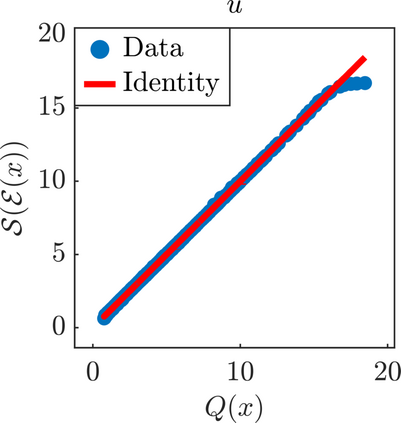
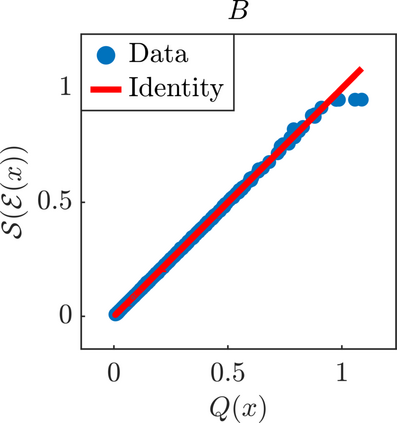
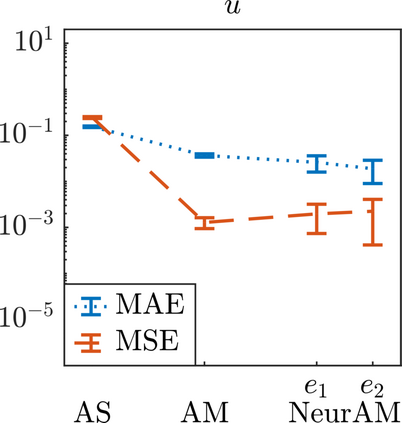
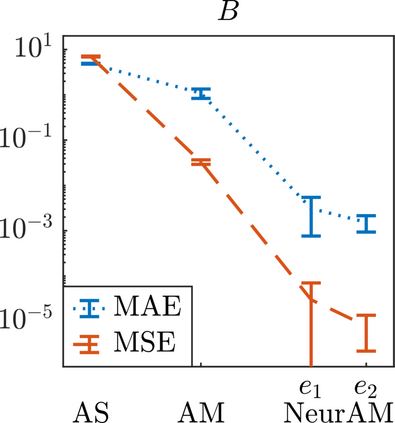
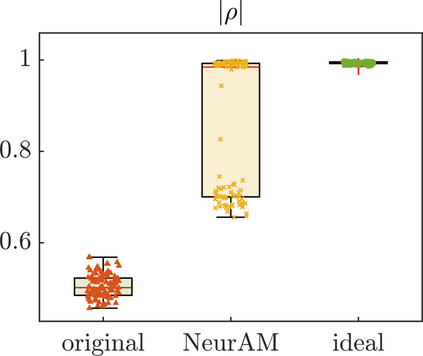
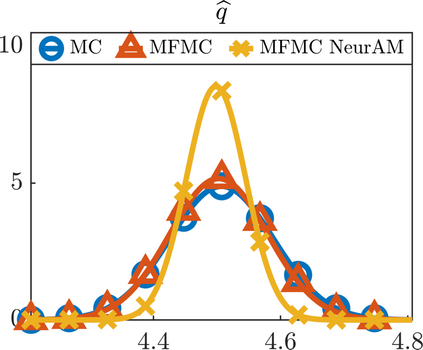
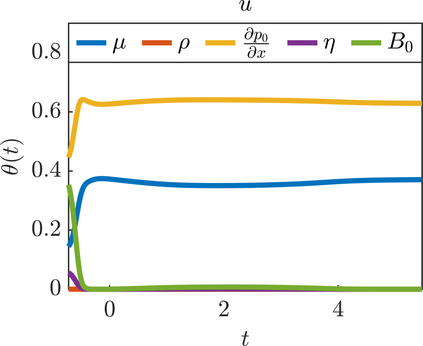
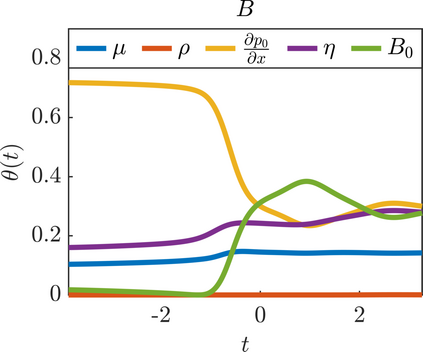
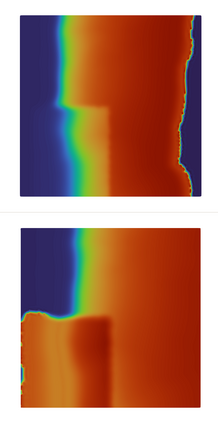
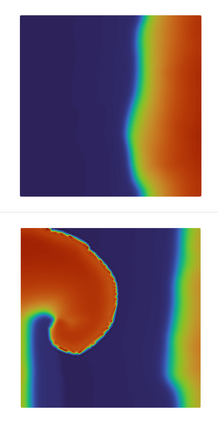
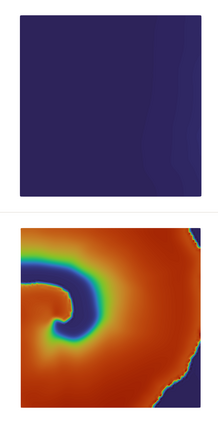
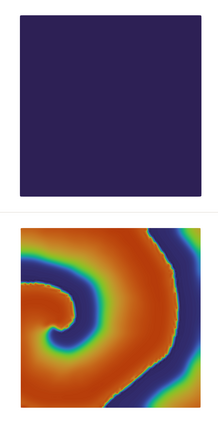
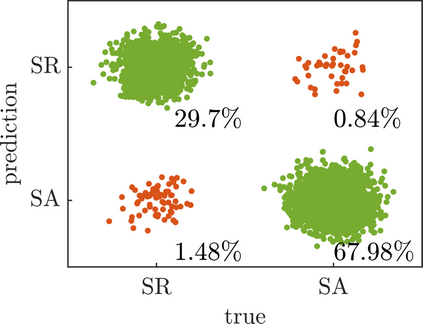
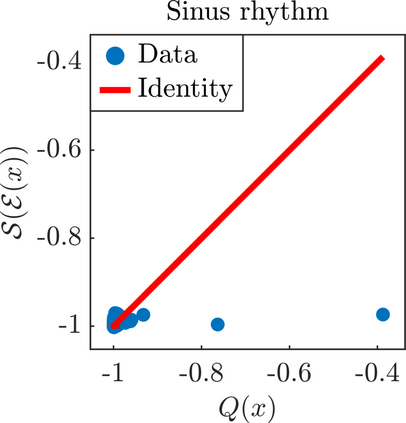
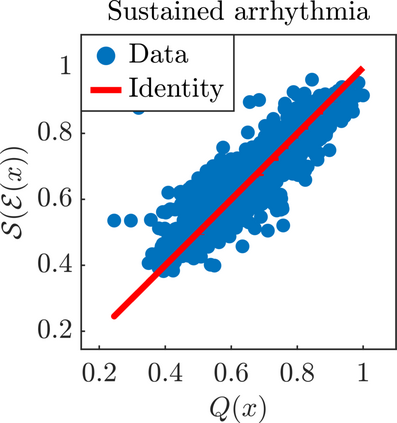
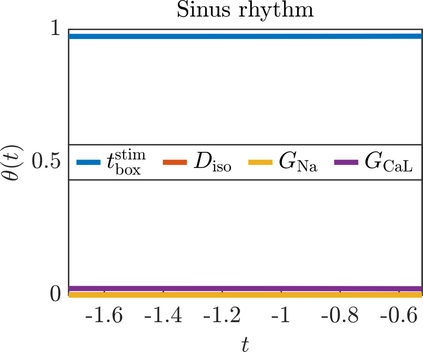
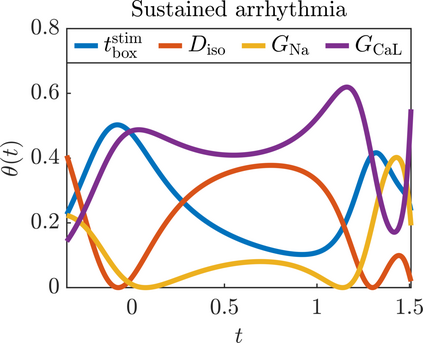
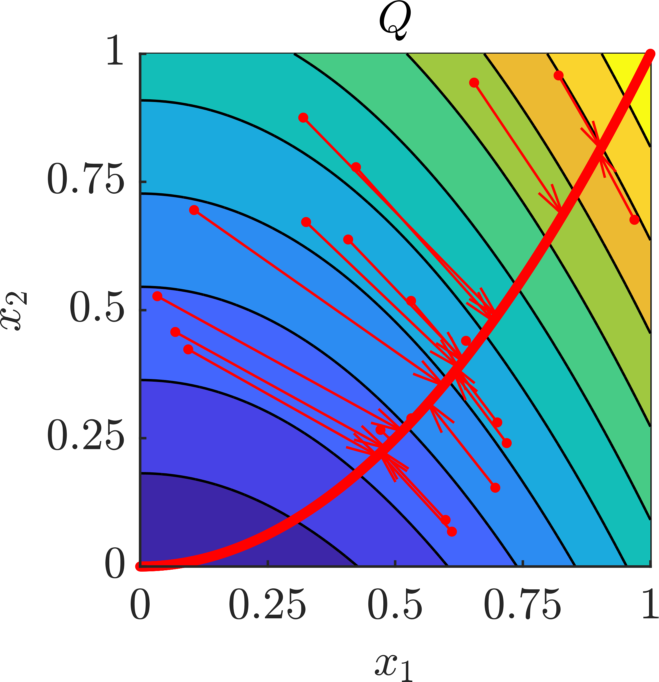
We present a new approach for nonlinear dimensionality reduction, specifically designed for computationally expensive mathematical models. We leverage autoencoders to discover a one-dimensional neural active manifold (NeurAM) capturing the model output variability, through the aid of a simultaneously learnt surrogate model with inputs on this manifold. Our method only relies on model evaluations and does not require the knowledge of gradients. The proposed dimensionality reduction framework can then be applied to assist outer loop many-query tasks in scientific computing, like sensitivity analysis and multifidelity uncertainty propagation. In particular, we prove, both theoretically under idealized conditions, and numerically in challenging test cases, how NeurAM can be used to obtain multifidelity sampling estimators with reduced variance by sampling the models on the discovered low-dimensional and shared manifold among models. Several numerical examples illustrate the main features of the proposed dimensionality reduction strategy and highlight its advantages with respect to existing approaches in the literature.

翻译：暂无翻译