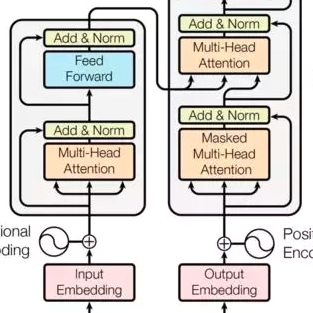
The strong lottery ticket hypothesis (SLTH) conjectures that high-performing subnetworks, called strong lottery tickets (SLTs), are hidden in randomly initialized neural networks. Although recent theoretical studies have established the SLTH across various neural architectures, the SLTH for transformer architectures still lacks theoretical understanding. In particular, the current theory of the SLTH does not yet account for the multi-head attention (MHA) mechanism, a core component of transformers. To address this gap, we introduce a theoretical analysis of the existence of SLTs within MHAs. We prove that, if a randomly initialized MHA of $H$ heads and input dimension $d$ has the hidden dimension $O(d\log(Hd^{3/2}))$ for the key and value, it contains an SLT that approximates an arbitrary MHA with the same input dimension with high probability. Furthermore, by leveraging this theory for MHAs, we extend the SLTH to transformers without normalization layers. We empirically validate our theoretical findings, demonstrating that the approximation error between the SLT within a source model (MHA and transformer) and an approximate target counterpart decreases exponentially by increasing the hidden dimension of the source model.

翻译：强彩票假说（SLTH）认为，在随机初始化的神经网络中隐藏着高性能的子网络，称为强彩票（SLT）。尽管近期的理论研究已在多种神经架构中证实了SLTH，但对于Transformer架构的SLTH仍缺乏理论理解。具体而言，当前SLTH理论尚未涵盖多头注意力（MHA）机制——Transformer的核心组件。为填补这一空白，我们对MHA中SLT的存在性进行了理论分析。我们证明，若一个具有$H$个头、输入维度$d$的随机初始化MHA，其键和值的隐藏维度为$O(d\\log(Hd^{3/2}))$，则该MHA以高概率包含一个可近似任意具有相同输入维度的MHA的SLT。进一步地，通过将此MHA理论拓展，我们将SLTH延伸至无归一化层的Transformer架构。我们通过实验验证了理论结果，表明源模型（MHA及Transformer）中的SLT与近似目标模型之间的逼近误差，随源模型隐藏维度的增加呈指数级下降。