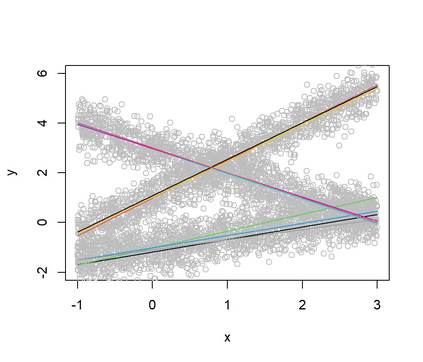
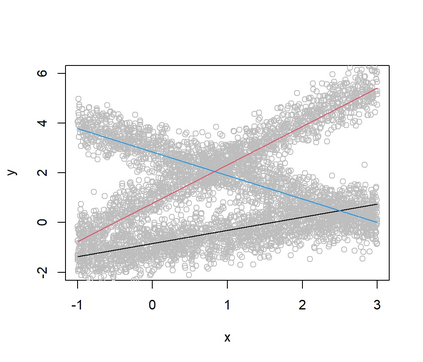
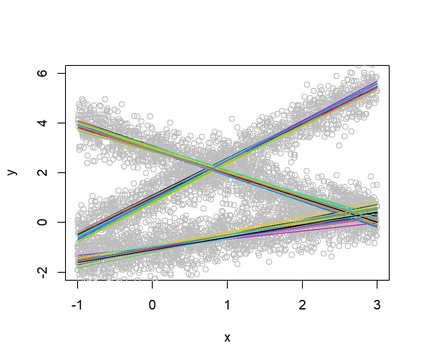
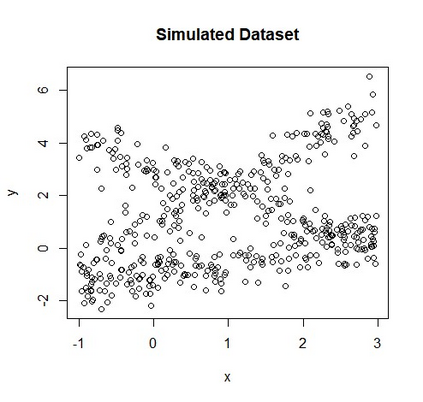
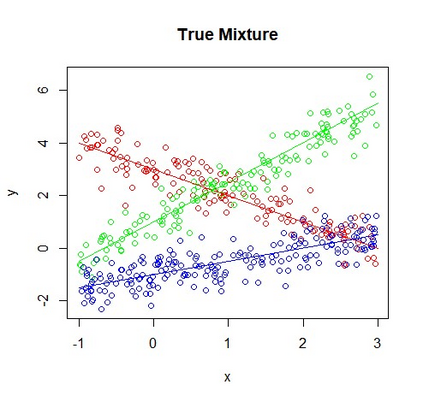
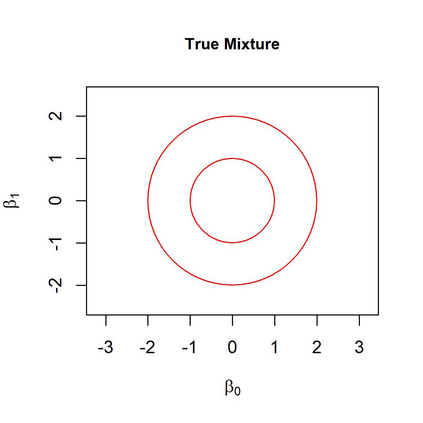
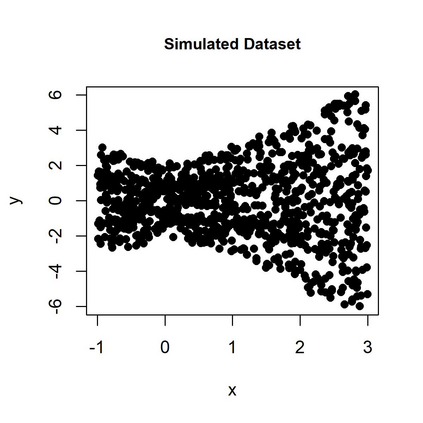
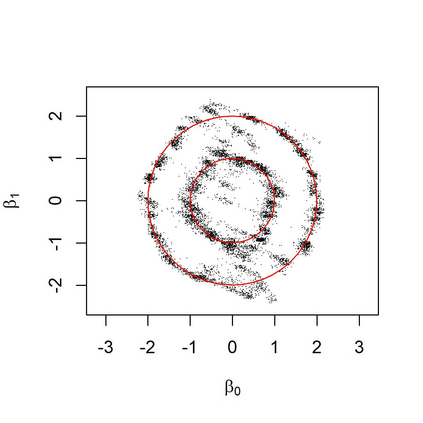
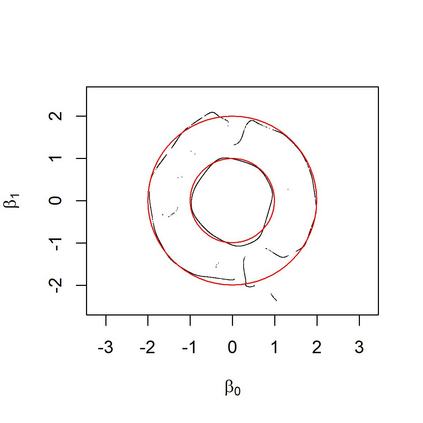
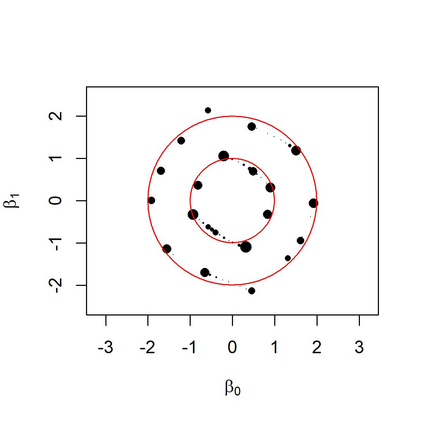
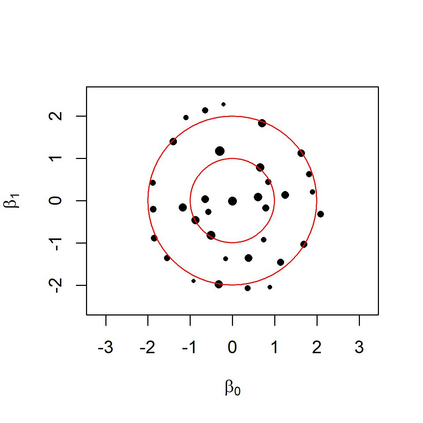
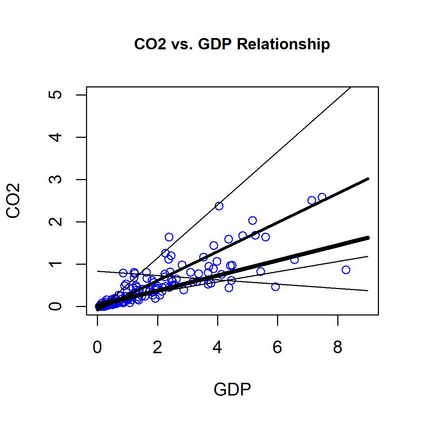
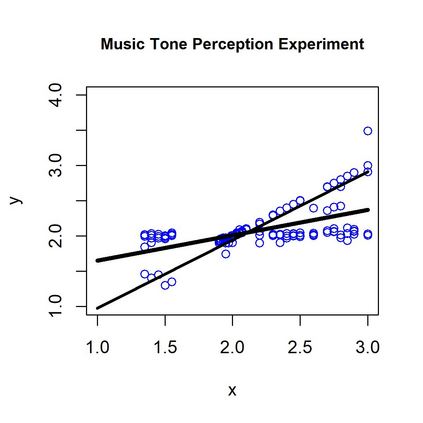
In a mixture of linear regression model, the regression coefficients are treated as random vectors that may follow either a continuous or discrete distribution. We propose two Expectation-Maximization (EM) algorithms to estimate this prior distribution. The first algorithm solves a kernelized version of the nonparametric maximum likelihood estimation (NPMLE). This method not only recovers continuous prior distributions but also accurately estimates the number of clusters when the prior is discrete. The second algorithm, designed to approximate the NPMLE, targets prior distributions with a density. It also performs well for discrete priors when combined with a post-processing step. We study the convergence properties of both algorithms and demonstrate their effectiveness through simulations and applications to real datasets.

翻译：暂无翻译