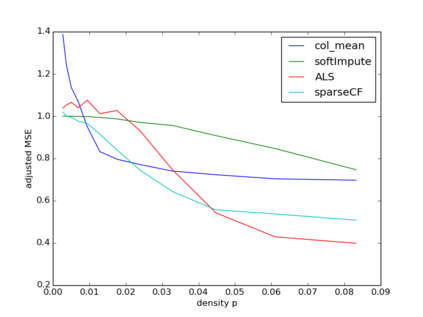
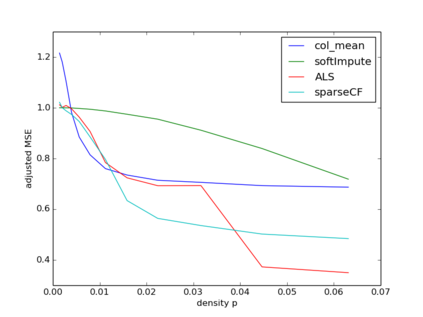
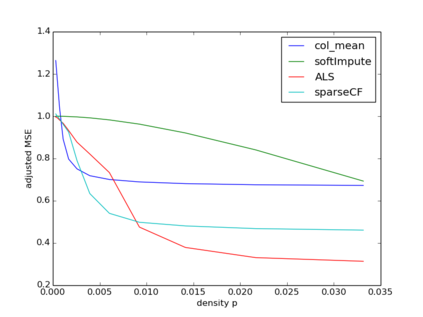
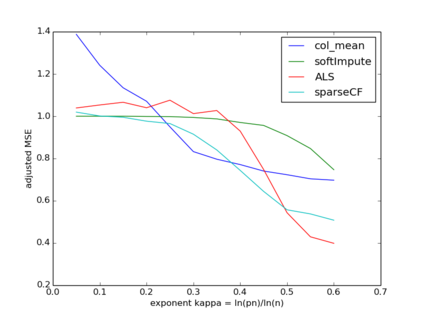
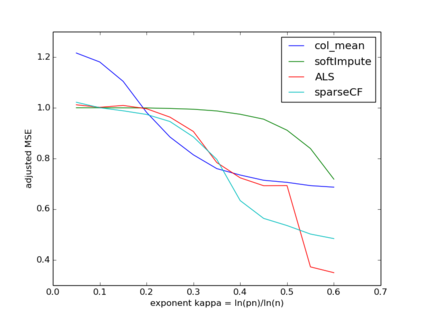
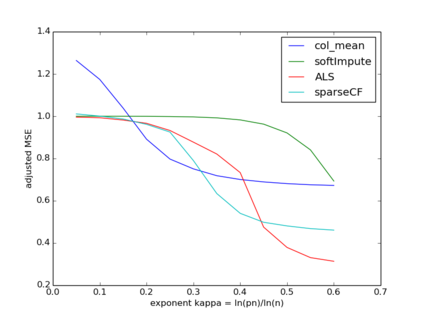
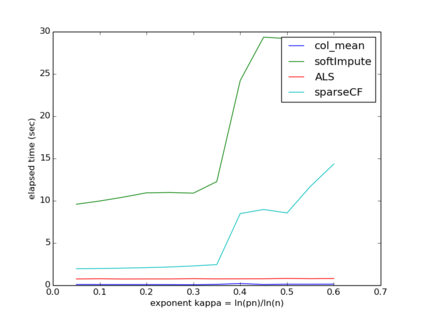
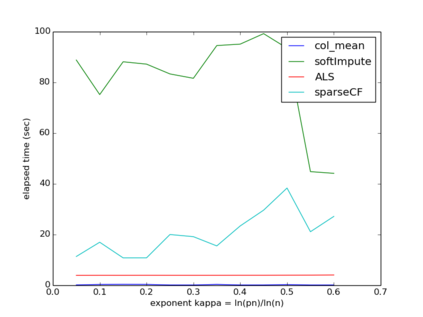
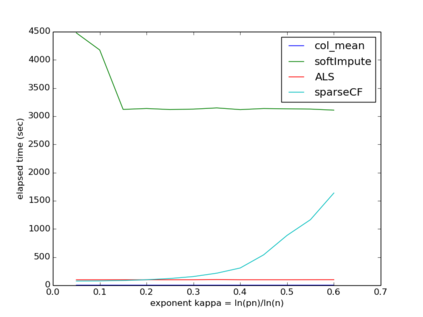
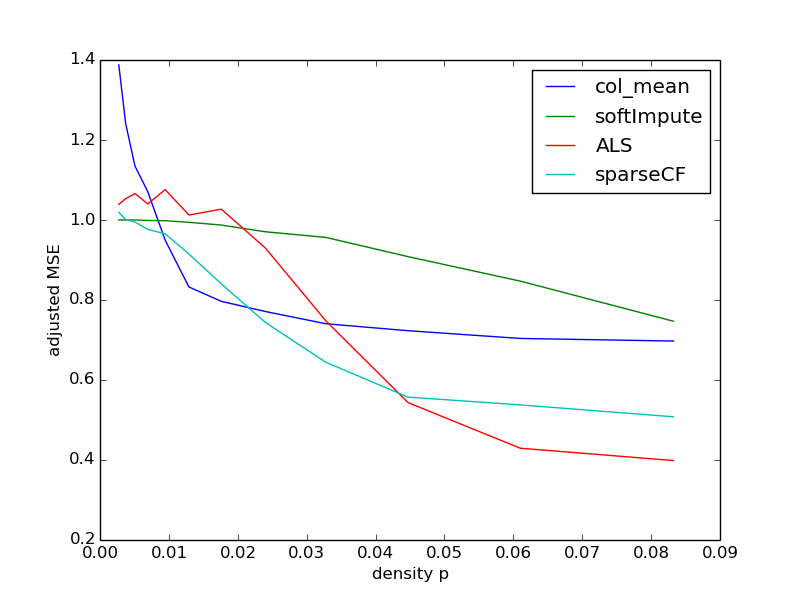
We consider sparse matrix estimation where the goal is to estimate an $n\times n$ matrix from noisy observations of a small subset of its entries. We analyze the estimation error of the popularly utilized collaborative filtering algorithm for the sparse regime. Specifically, we propose a novel iterative variant of the algorithm, adapted to handle the setting of sparse observations. We establish that as long as the fraction of entries observed at random scale as $\frac{\log^{1+\kappa}(n)}{n}$ for any fixed $\kappa > 0$, the estimation error with respect to the $\max$-norm decays to $0$ as $n\to\infty$ assuming the underlying matrix of interest has constant rank $r$. Our result is robust to model mis-specification in that if the underlying matrix is approximately rank $r$, then the estimation error decays to the approximate error with respect to the $\max$-norm. In the process, we establish algorithm's ability to handle arbitrary bounded noise in the observations.

翻译：我们考虑的是稀少的矩阵估计,其中的目标是从对一小部分条目的杂音观测中估算一个美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=10美元=0=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=13=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10=10