题目： Topological Bayesian Optimization with Persistence Diagrams

摘要：

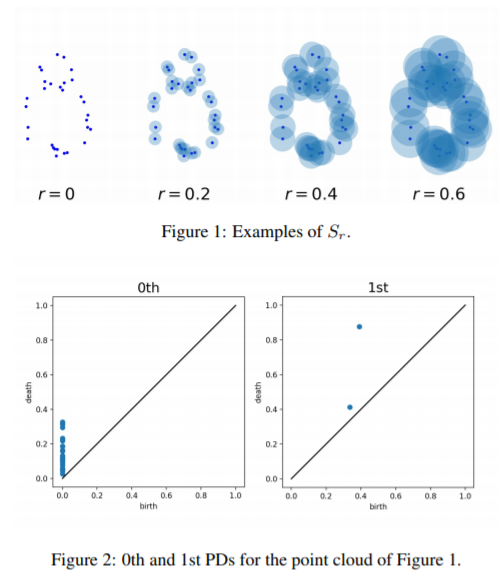
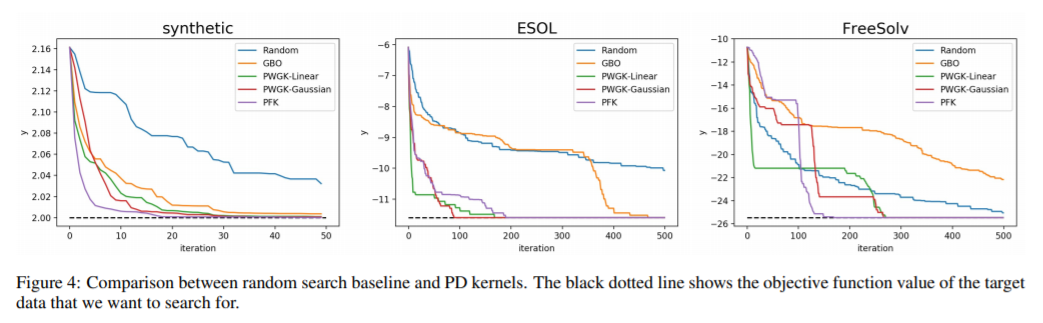
寻找黑盒函数的最优参数对于寻找稳定的材料结构和最优的神经网络结构具有重要意义，贝叶斯优化算法在这方面得到了广泛的应用。然而，现有的贝叶斯优化算法大多只能处理向量数据，不能处理复杂的结构化数据。在本文中，我们提出了拓扑贝叶斯优化，它可以有效地利用拓扑信息从结构化数据中找到最优解。更具体地说，为了将贝叶斯优化应用于结构化数据，我们从结构中提取有用的拓扑信息，并测量结构之间的适当相似性。为此，我们利用了持久同源性，这是一种拓扑数据分析方法，最近被应用于机器学习。此外，我们还提出了贝叶斯优化算法，该算法通过对持久性图使用内核的线性组合来处理多种类型的拓扑信息。实验结果表明，与随机搜索基线和图贝叶斯优化算法相比，基于持久同源性提取的拓扑信息能更有效地搜索最优结构。