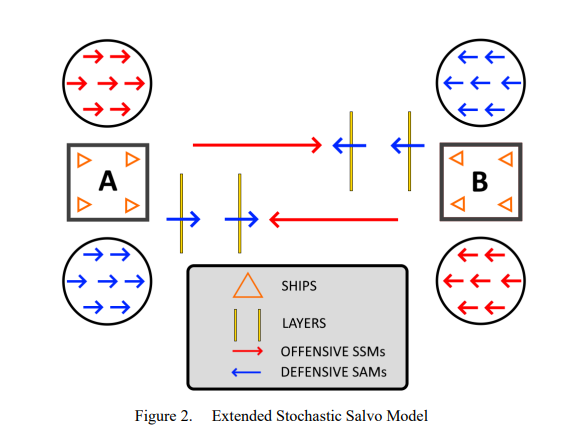
Hughes开发了首个齐射作战模型，该模型通过数学方法模拟军舰间多枚导弹协同齐射的作战行为。Armstrong在此基础上发展了该模型的随机版本，将概率与统计要素纳入模型框架。然而与休斯模型相似，Armstrong模型仍保留若干简化假设：仅模拟单轮交战、假定所有导弹均在单轮发射、未考虑分层防御体系、且不追踪导弹库存状态。本论文通过矩阵实验室（MATLAB）实现系列改进以提升模型精度与真实性，从而扩展了阿姆斯特朗模型。改进措施在矩阵实验室环境中实施，涵盖多轮齐射动态机制、分层导弹防御系统、导弹库存耗尽模拟及部分库存使用策略。该扩展模型采用蒙特卡洛方法求解平均效能指标，包括获胜概率、未被拦截导弹平均数量、幸存舰艇平均数量及一方被消灭前的平均交战轮次。无论在势均力敌还是不对称作战情境中，尽早获得数量优势对改变战局至关重要。实验结果表明：与防御能力相比，强化进攻能力对提高获胜概率和降低未被拦截导弹数量具有更显著影响。此外，实验结果证明该模型可用于在成本约束下对不同军舰属性（包括进攻能力、防御能力和持续作战能力）进行权衡分析。该实验成果展示了决策者如何运用此模型设定预算与预期效能度量阈值，并通过实验设计来寻找最具成本效益的军舰属性配置方案。